真偽 とは
基本情報技術者 過去問 2019年 春期 午前 問3 を参考に考えてみます。
<問題>
P,Q,Rはいずれも命題である。命題Pの真理値は真であり,命題 (not P) or Q 及び命題 (not Q) or R のいずれの真理値も真であることが分かっている。Q,Rの真理値はどれか。ここで,X or Y は X と Y の論理和,not X は X の否定を表す。
(ア) Q:偽 R:偽
違いますよ。ベン図知ってます?勉強しなおしたら?
(イ) Q:偽 R:真
高校数学からやり直したほうがいいかもしれませんね。違いますよ。
(ウ) Q:真 R:偽
ちゃうちゃう。ちゃうちゃうとちゃうちゃう。
(エ) Q:真 R:真
正解です!カンじゃないですよね?冗談です。さすがです。
P,Q,Rはいずれも命題である。命題Pの真理値は真であり,命題 (not P) or Q 及び命題 (not Q) or R のいずれの真理値も真であることが分かっている。Q,Rの真理値はどれか。ここで,X or Y は X と Y の論理和,not X は X の否定を表す。
ここから私の思考です↓
ちなみに青字は文章を読んだ際の私の頭の中です。
<問題>
P,Q,Rはいずれも命題である。命題Pの真理値は真であり,命題 (not P) or Q 及び命題 (not Q) or R のいずれの真理値も真であることが分かっている。Q,Rの真理値はどれか。ここで,X or Y は X と Y の論理和,not X は X の否定を表す。
高校数学でこんなのあったかな?真の反対が偽で・・・
高校数学? ベン図?めっちゃ懐かしいな。覚えてるかな俺。
「or または」 ってことは 合わせたところで、
「not じゃない」 ってことは まんまそこ以外ってことね。
絵で描いたほうがわかるかな?
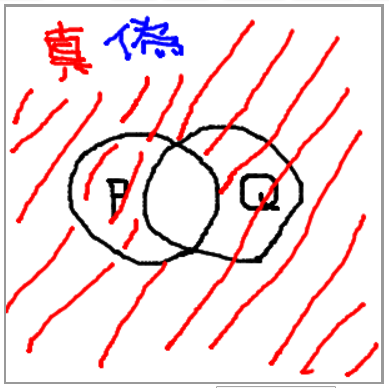
命題Pが真だから「命題 (not P) or Q」が真ならこんな感じか。
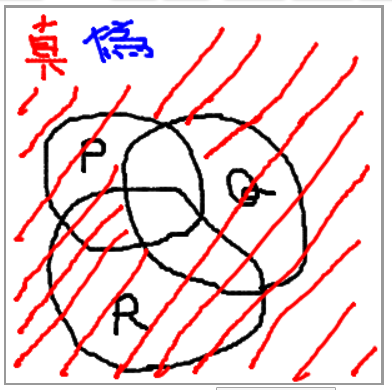
命題 (not Q) or R も真だから、さっきのと合わすとこんなかんじ?
これを元にすればいいんかな?てかほとんど真やん。合ってんのこれ?
(ア) Q:偽 R:偽
QもRも真だから違う。
(イ) Q:偽 R:真
QもRも真だから違う。
(ウ) Q:真 R:偽
QもRも真だから違う。
(エ) Q:真 R:真
QもRも真だからこれじゃない?
正解は(エ)!
正解は(エ)です。
おお!!当たった!!
真偽とは、ベン図を書いたらわかります。高校数学の数Aで出てきたあれですね。
今回は特にありません。パチパチパチ。
また1つ賢くなりました。よかったよかった。



コメント