アルゴリズム問題は実際に数字を入れてみましょう
基本情報技術者 過去問 2019年 春期 午前 問1 を参考に考えてみます。
基本情報技術者試験 2019年 秋 午前 問1 を考えてみましょう。
<問題>
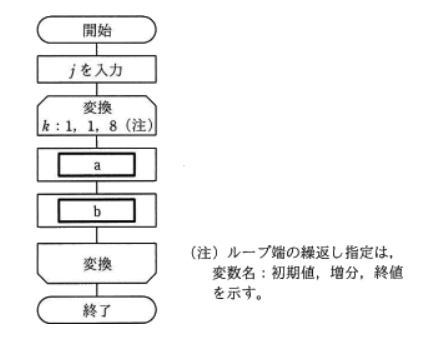
次の流れ図は,10進整数 j(0<j<100) を8桁の2進数に変換する処理を表している。2進数は下位桁から順に,配列の要素 NISHIN(1) から NISHIN(8) に格納される。流れ図のa及びbに入る処理はどれか。ここで,j div 2 はjを2で割った商の整数部分を,j mod 2 はjを2で割った余りを表す。
<選択肢>
次の流れ図は,10進整数 j(0<j<100) を8桁の2進数に変換する処理を表している。
ここからは私の思考です↓
ちなみに青字は文章を読んだ際の私の頭の中です。
次の流れ図は,10進整数 j(0<j<100) を8桁の2進数に変換する処理を表している。
はいはい、10進数から2進数への変換ね。2でずっと割っていくやつね。わかりますよ。
2進数は下位桁から順に,配列の要素 NISHIN(1) から NISHIN(8) に格納される。
JAPANESE NISHIN. I love NISHIN!
下位から順にってことはこういうことね。
NISHIN(8) NISHIN(7) NISHIN(6) NISHIN(5) NISHIN(4) NISHIN(3) NISHIN(2) NISHIN(1)
流れ図のa及びbに入る処理はどれか。ここで,j div 2 はjを2で割った商の整数部分を,j mod 2 はjを2で割った余りを表す。
こうやって div とか mod とかを問題文に使うから文系は難しいと感じてしまう気がしますね
こういうのは具体例をいれていくのが一番な気がする。
好きな数字でも入れていこうか。
私は「7」という数字が好きなので「7」をいれることにします。
ちなみに「7」を8ケタの2進数で表すと「00000111」だから
計算結果がこうなればいいわけよね。
入れるのは少なめの数値にしたほうが計算が楽ですよ
では具体的にアから順にみていこうかな。
「ア」
開始
↓
j を入力 【 7を入力 】
↓
k:1,1,8 【kは1】
j ← j div 2 【j ← 7÷2 つまり j は3.5の整数部分の3】
↓
NISHIN(k) = j mod 2 【NISHIN(1) ← 3÷2 の余り つまり
NISHIN(1)は1】
↓
k:1,1,8 【kは2】
↓
j ← j div 2 【j ← 3÷2 つまり j は1.5の整数部分の1】
↓
NISHIN(k) = j mod 2 【NISHIN(2) ← 1÷2 の余り つまり
NISHIN(2)は1】
↓
k:1,1,8 【kは3】
j ← j div 2 【j ← 1÷2 つまり j は0.5の整数部分の0】
↓
NISHIN(k) = j mod 2 【NISHIN(3) ← 0÷2 の余り つまり
NISHIN(3)は0】
おや、こっからは全部NISHIN(k)は0だね。
ってことは00000011。「ア」は違うね。
では続いて「イ」を順にみていきますか。
開始
↓
j を入力 【7を入力】
↓
k:1,1,8 【kは1】
j ← j mod 2 【j ← 7÷2の余り つまり j は1】
↓
NISHIN(k) = j div 2 【NISHIN(1) ← 1÷2 つまり0.5の整数部分
NISHIN(1)は1】
↓
k:1,1,8 【kは2】
↓
j ← j mod 2 【j ← 1÷2の余り つまりjは1】
↓
NISHIN(k) = j div 2 【NISHIN(1) ← 1÷2 つまり0.5の整数部分
NISHIN(2)は0】
↓
k:1,1,8 【kは3】
↓
j ← j mod 2 【j ← 1÷2の余り つまりjは1】
↓
NISHIN(k) = j div 2 【NISHIN(1) ← 1÷2 つまり0.5の整数部分
NISHIN(3)は0】
ここまできたら後は同じなので00000001となるので「イ」も違う。次!!!
続いて「ウ」をみていきます。
開始
↓
j を入力 【7を入力】
↓
k : 1,1,8 【kは1】
↓
NISHIN(k) ← j div 2 【7÷2の整数部分 なのでNISHIN(1)は3】
はい、きた!2進数なのに3が来てるからもう「ウ」はダメですね。
、、、
ってことはもう残るのは1つなので正解は「エ」ということになるはずですが
一応順にみていきましょうか。
「エ」
開始
↓
j を入力 【7を入力】
↓
k : 1,1,8 【kは1】
↓
NISHIN(k) ← j mod 2 【7÷2の余り なのでNISHIN(1)は1】
↓
j ← j div 2 【7÷2の整数部分なので jは3】
↓
k : 1,1,8 【kは2】
↓
NISHIN(k) ← j div 2 【3÷2の整数部分なので NISHIN(2)は1】
↓
j ← j div 2 【3÷2の整数部分なので j は1】
↓
k :1,1,8 【kは3】
↓
NISHIN(k) ← j mod 2 【1÷2の余り つまりNISHIN(3)は1】
↓
j ← j div 2 【1÷2の整数部分なのでjは0】
ここまでくるとあとは全部0なので
00000111となる。やっぱりこれが正解やね。
ということで正解は「エ」!!!
正解は「エ」です。
よっしゃ!!!今回は完璧でしょう。
こういう問題は実際に具体的に数字を当てはめて考えてみるに限りますね。
ではこの辺で終わります。
最後まで読んでいただいてありがとうございました。
引き続き勉強頑張っていきましょう。








コメント
イの
NISHIN(k) = j div 2 【NISHIN(1) ← 1÷2 つまり0.5の整数部分
NISHIN(1)は 1
NISHIN(1)はなぜ 1 になったのでしょうか?
ご指摘ありがとうございます。
ほんとですね。整数部分は「1」ではなく「0」ですね。
間違ってます。