ビットを反転させてみるかね
基本情報技術者試験 2019年 秋 午前 問2 を考えてみましょう。
<問題>
8ビットの値の全ビットを反転する操作はどれか。
(ア) 16進表記 00 のビット列と排他的論理和をとる。
(イ) 16進表記 00 のビット列と論理和をとる。
(ウ) 16進表記 FF のビット列と排他的論理和をとる。
(エ) 16進表記 FF のビット列と論理和をとる。
8ビットの値の全ビットを反転する操作はどれか。

ここから私の思考です↓
ちなみに青字は文章を読んだ私の頭の中です。
<問題>
8ビットの値の全ビットを反転する操作はどれか。
8ビットの値の全ビットを反転とな?計算問題は正直苦手ですね。
あと、練習不足で覚えていない。まぁ読み進めていきましょう。
(ア) 16進表記 00 のビット列と排他的論理和をとる。
他の選択肢も見る限り、それぞれまず2進数に変換する必要があるな。
16進数の00をまず10進数に直すと、
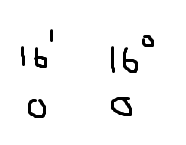
0だね。んで0を2進数8ビット表記にすると
00000000だね。
これとの排他的論理和、、、
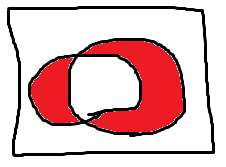
どっちかが1のときだけ1を返すのね。
仮に元の数値が01010101なら
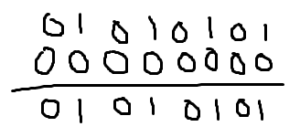
00000000の排他的論理和って反転にはならんな。(ア)は違う。
え?全選択肢をこんな感じで進めんの?めんどくさ。
(イ) 16進表記 00 のビット列と論理和をとる。
さて次、さっきと一緒で00000000だね。
論理和だから
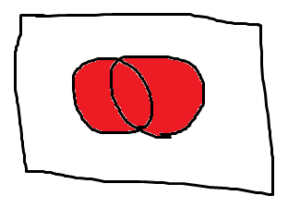
どっちかが1なら1を返すと。
00000000の論理和、、、
仮に元の数値が01010101だとすると

00000000の論理和は反転にはならない。(イ)も違う。
(ウ) 16進表記 FF のビット列と排他的論理和をとる。
FFを10進数にすると
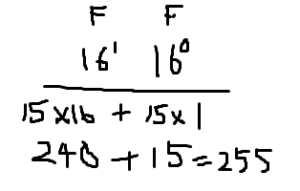
255を2進数にすると
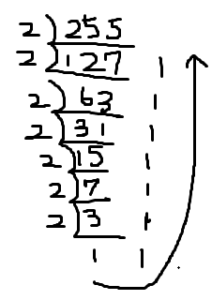
11111111となる。
排他的論理和か。

仮に元の数値を01010101とすると
01010101と11111111との排他的論理和は
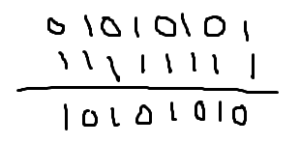
おお!反転した!答えはわかったけど、一応(エ)も考えておこうか。
(エ) 16進表記 FF のビット列と論理和をとる。
さっき求めたからわかるわ。16進数のFFは2進数だと11111111。
論理和は
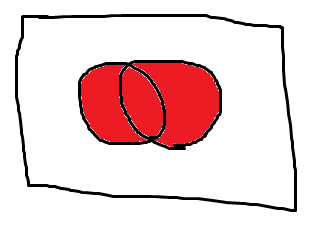
仮に元の数値を01010101とすると
11111111と01010101の論理和は
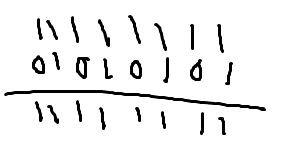
となるので違いますね。
ということで、正解は(ウ)で決定!!
正解は(ウ)です。
よっしゃ、今回は完璧ですね。
計算問題を苦手としながらも今回は完璧だったのではないでしょうか。
ここ最近全然勉強してなかったからやばいな。
勉強しなおしていかないと。
最後まで読んでいただいてありがとうございました
引き続き勉強頑張りましょうね。






コメント