ノードやエッジって意味がわからなくても読み進めましょう
基本情報技術者試験 2019年 秋 午前 問3 を考えてみましょう。
<問題>
ノードとノードの間のエッジの有無を,隣接行列を用いて表す。ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。
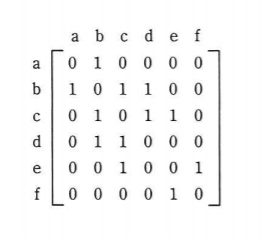

ノードとノードの間のエッジの有無を,隣接行列を用いて表す。
ここから私の思考です↓
ちなみに青字は文章を読んだ私の頭の中です。
<問題>
ノードとノードの間のエッジの有無を,隣接行列を用いて表す。
ノードってパソコンとかのことだったかな?エッジって何?わからんけど読み進めよう。隣接行列?もよくわからんけど下に記載してある行列の形をそう言うんかね。
ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。
無向グラフ?これも単語がわからん。こんなん参考書とかに出てきたかね?まぁ読み進めよう。
ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。
要はノード同士が繋がっている場合は1、繋がってないのは0ということでOK?
行列を見て1となっているところが線でつながっていると。行列と絵が合っているのを探せばええんやね。


グラフってこれのことを言ってるんかね?グラフって聞いたら普通さ、折れ線グラフとか棒グラフとかをイメージしちゃうよね。こんなのもグラフと呼ぶのか。
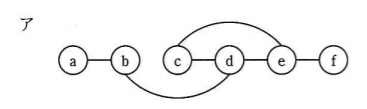
行列を見ていくと、 b と c の交わるところが 1 になってるけど、グラフでは線が繋がっていないから(ア)は違うな。


続きまして(イ)を見ていきます。
おかしなところ、おかしなところ、
c と d の交わるところが 1 になってるけど、グラフでは繋がっていないな。ということで(イ)も違う。


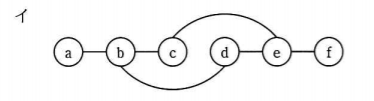
おかしなところ、おかしなところ、、、
ない!全部正しい!ということはこれが正解やな。
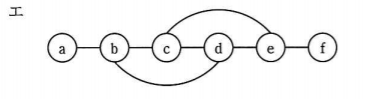
けど、せっかくなので(エ)も見るだけみておきましょう。どうせ違うけどね。


d と e の交わるところが 0 になっているのにグラフでは繋がっている。
行列ではなしで、グラフではありパターンのやつか!
でも(ウ)で正解がわかってしまう人が多いやろし、(エ)に関しては見てももらえないことも多いんやろね。
かわいそうな問題ですこと。
ということで正解は(ウ)!!
正解は(ウ)です。
よっしゃ!わからん部分があったとしても読み進めたらなんとかなることもあるね。
ノードってまぁ、パソコンのことでしょ。

最後まで読んでいただいてありがとうございました。
今後も引き続き勉強頑張りましょうね。
私も頑張ります。








コメント