流れ図の問題は実際にサンプルを取って確認してみましょう
基本情報技術者 過去問 2019年(令和元年) 秋期 午前 問9 を参考に考えてみます。
<問題>
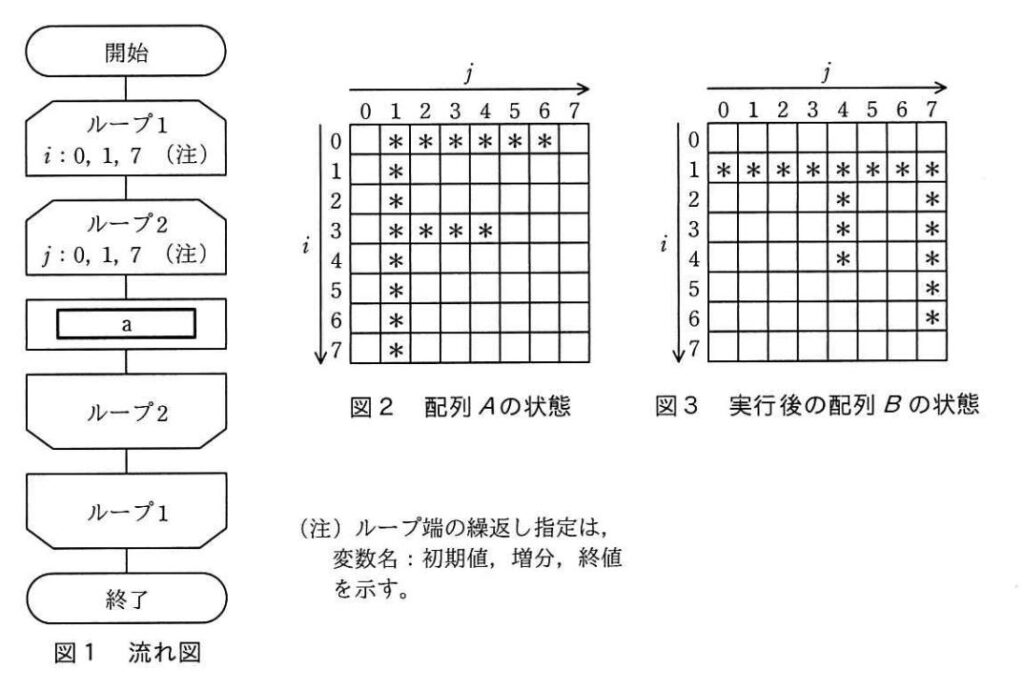
配列Aが図2の状態のとき,図1の流れ図を実行すると,配列Bが図3の状態になった。
図1のaに入れるべき操作はどれか。
ここで,配列A,Bの要素をそれぞれ A(i,j),B(i,j) とする。
<選択肢>
(ア) B(7-i,7-j) ← A(i,j)
(イ) B(7-j,i) ← A(i,j)
(ウ) B(i,7-j) ← A(i,j)
(エ) B(j,7-i) ← A(i,j)

配列Aが図2の状態のとき,図1の流れ図を実行すると,配列Bが図3の状態になった。図1のaに入れるべき操作はどれか。ここで,配列A,Bの要素をそれぞれ A(i,j),B(i,j) とする。
ここから私の思考です↓
ちなみに青字は文章を読んだ際の私の頭の中です。
<問題>
配列Aが図2の状態のとき,図1の流れ図を実行すると,配列Bが図3の状態になった。
うん、90度時計回りに回転してますね。
図1のaに入れるべき操作はどれか。
知らんがな。クリっとする。コテっとする。以上。
ここで,配列A,Bの要素をそれぞれ A(i,j),B(i,j) とする。
はいはい、1つずつ順番に当てはめていけばいいんでしょ。くそめんどくせぇ。

ほんとこういう問題が午前で出題されるとめんどくさいですね。
どの問題も1.25点なんだから、こんな時間のかかりそうな問題は正直後回しにします。
マジで一番最後に解くくらいの問題かもしれませんね。
だってみるからにめんどくさそうですもん。
けどまぁ順番に1個1個進めていくしかないですね。
まず、

これの意味。よく見ると意味がご丁寧に書いてますね。
(注)ループ端の繰り返し指定は、変数名:初期値、増分、終値を示す。
ということは上記のやつは、
iは0から1ずつ増えてって、7で終わりってことですね。
ループ2も一緒。ループ2のjも同じ。
ループ2はループ1の中にあるから、jが0~7まで増えるとiが1増えるって感じね。
てかiとjってわかりにくいな。
なんでわざわざこんな見間違えそうな文字を使うかな。
数字の0とアルファベットのOを使う問題とかも嫌いですね。
こすい問題ですこと。
<選択肢>
(ア) B(7-i,7-j) ← A(i,j)
あてずっぽで3点くらいを調べたら判断できんじゃない?全部トレースなんてしてらんないしね。めんどくさいし。
ってことで、3点決めます。
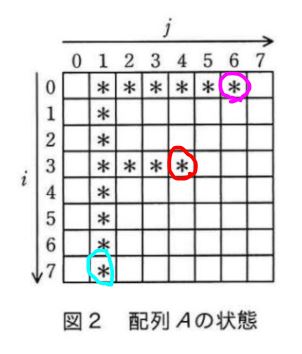
なんとなくこの3点にしましょう。端っこでわかりやすいし。
フィーリングですね、フィーリング。
ピンク丸から確認しましょうか。
B(7-i,7-j)←A(i,j)だから、
ピンク丸のところは*印がついているから、iとjに同じ数字をいれたとき、Bにも*印がついていたらいいね。
Aのピンク丸はi=0、j=6です。ということは
B(7-0,7-6) = B(7,1) なので、Bのi=7、j=1のところが*印であれば合格と。
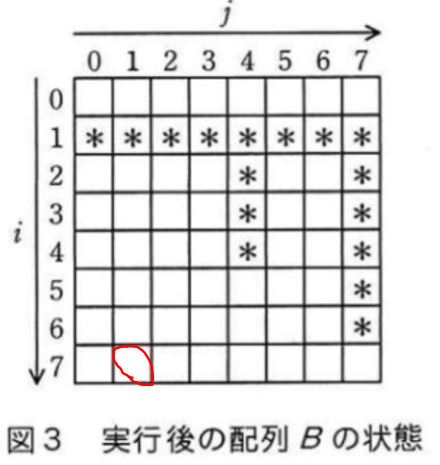
うん、*印はないですね。ということで(ア)は間違い。
次!
(イ) B(7-j,i) ← A(i,j)
同様に順番に確認していくだけですね。

Aのピンク丸はi=0、j=6です。ということは
B(7-6,0) = B(1,0) なので、Bのi=1、j=0のところが*印であれば合格と。
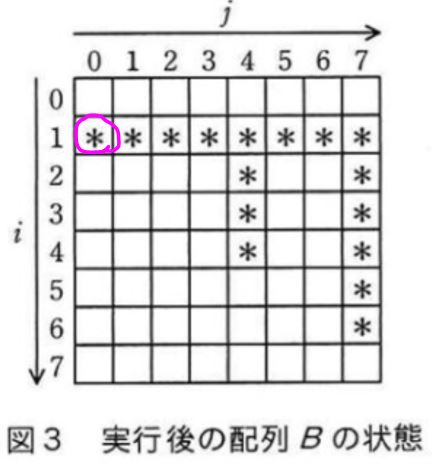
あった、ピンク丸のところはちゃんと*印がありました。では次の赤丸を同様に見てみましょうか。

Aにおいてi=3,j=4ということは
B(7-4,3) =B(3,3)に*印があれば合格と。
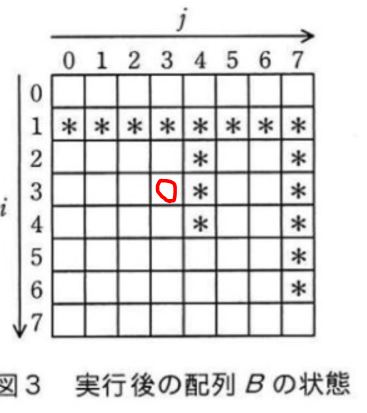
うん、ない!(イ)も違う。
(ウ) B(i,7-j) ← A(i,j)
同様に確認。

Aのピンク丸はi=0、j=6です。ということは
B(0,7-6) = B(0,1) なので、Bのi=0、j=1のところが*印であれば合格と。
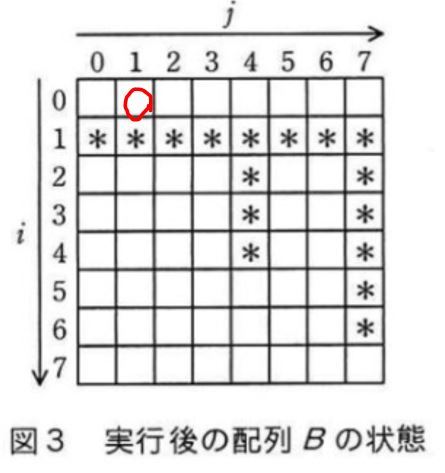
はい、(ウ)も違う。
ということで消去法で正解は残る(エ)ですね。
丁寧な解説の場合は正解とわかっていながらも一応正解であることを説明するんでしょうが、
テストは時間削減が大事です。
無駄なことに時間をかけている暇はありません。
そんなことなら思い切って決断し、次の問題を解くべし!
ということで正解は(エ)!
正解は(エ)です。
よっしゃ!ほらね。時間を無駄にしなくてすんだ。
今回は特に間違っている部分はありませんでしたね。
よかったよかった。
最後まで読んでいただきありがとうございました。
これからも勉強頑張ってくださいね。
私も勉強頑張ります。



コメント