ユークリッドの互除法 とは
基本情報技術者 過去問 2019年 春期 午前 問7を参考に考えてみます。
<問題>
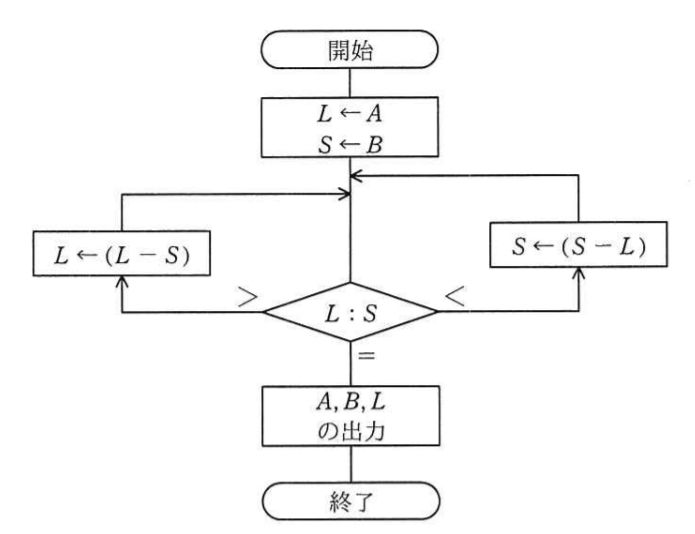
次の流れ図は,2数 A,B の最大公約数を求めるユークリッドの互除法を,引き算の繰返しによって計算するものである。Aが876,Bが204のとき,何回の比較で処理は終了するか。
<選択肢>
(ア) 4
(イ) 9
(ウ) 10
(エ) 11
次の流れ図は,2数 A,B の最大公約数を求めるユークリッドの互除法を,引き算の繰返しによって計算するものである。Aが876,Bが204のとき,何回の比較で処理は終了するか。
ここから私の思考です↓
ちなみに青字は文章を読んだ際の私の頭の中です。
<問題>
次の流れ図は,2数 A,B の最大公約数を求めるユークリッドの互除法を,引き算の繰返しによって計算するものである。Aが876,Bが204のとき,何回の比較で処理は終了するか。
ユークリッドの互除法なんて知らんし。
けど条件が書いてあるしこれの通りに処理をしていけばいいだけでしょう。
順番に処理を進めます。
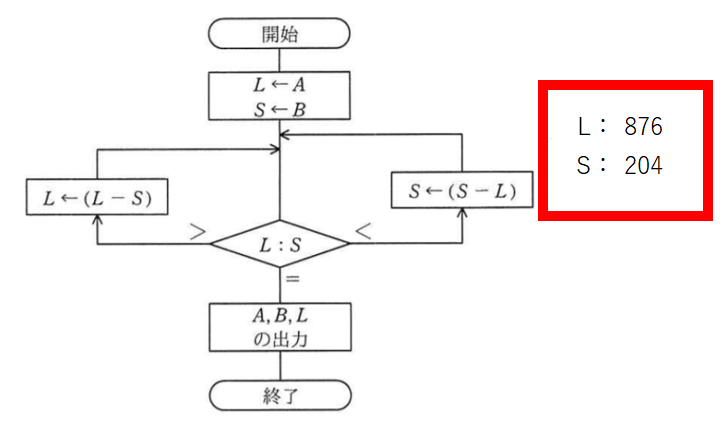
説明文の通りLにAの876を、SにBの204を代入します。
明らかに真ん中のL:Sの部分が比較の部分なのでこの処理を何回したかってのが答えになるんですね。LとSを比較して、Lの方が大きければ黄色矢印の左へ、Sが大きければ青矢印の右へ進んで、数字を更新すると。
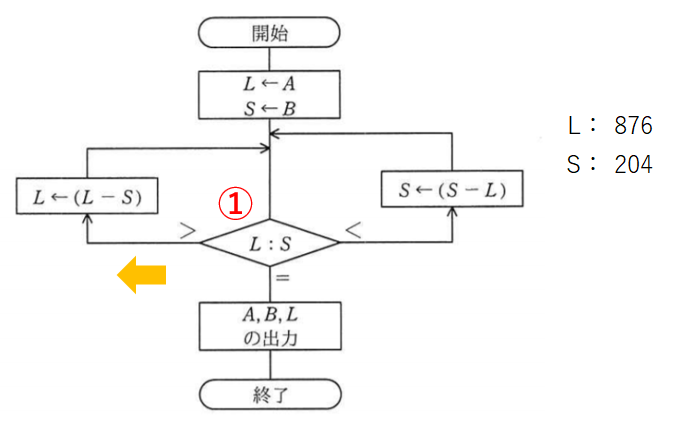
では1回目の比較です。
L876とS204なのでLが大きいので黄色矢印側の左に進みます。比較1回目
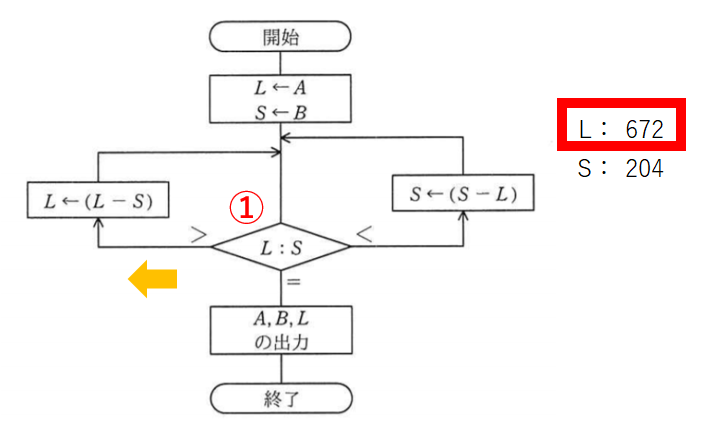
Lの672からSの204を引いて、Lを672にします。
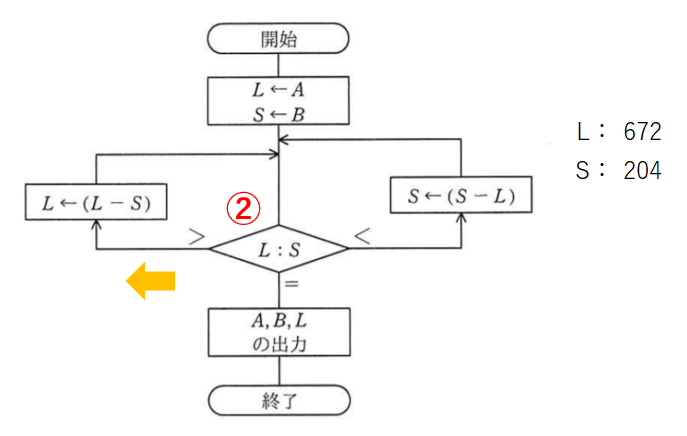
再度LとSを比較します。比較2回目。
Lの方が大きいのでまた矢印の左へ進みます。
Lの672からSの204を引いてLを468にします。
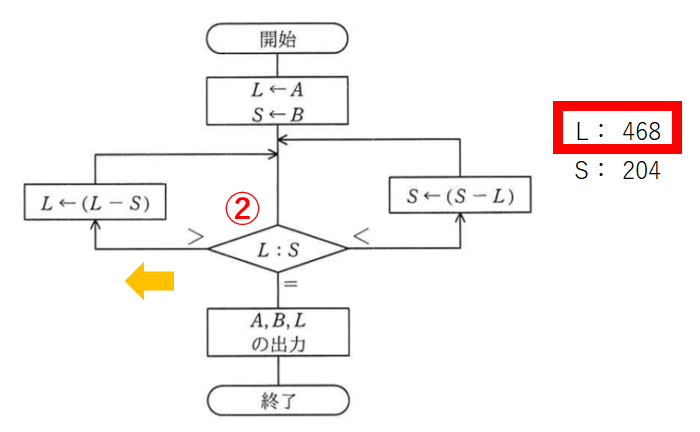
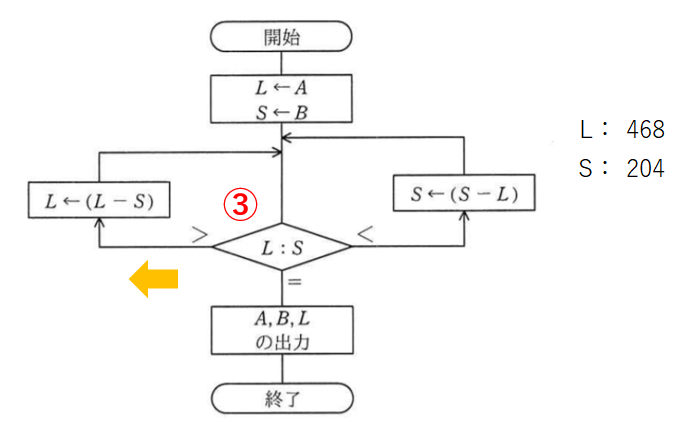
比較3回目。これも左側へ。
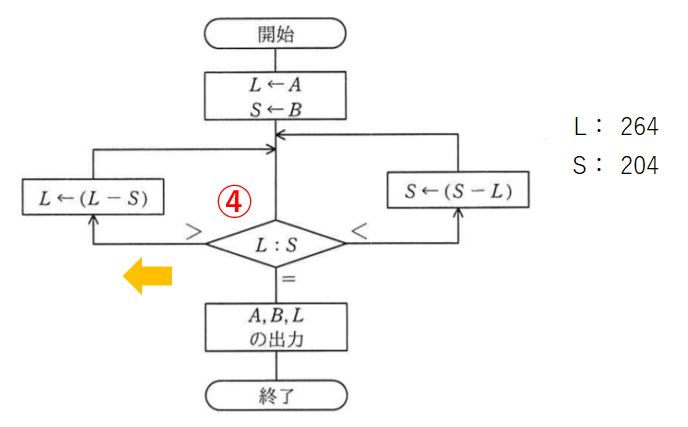
これまで同様にLからSを引いて、Lを264にします。
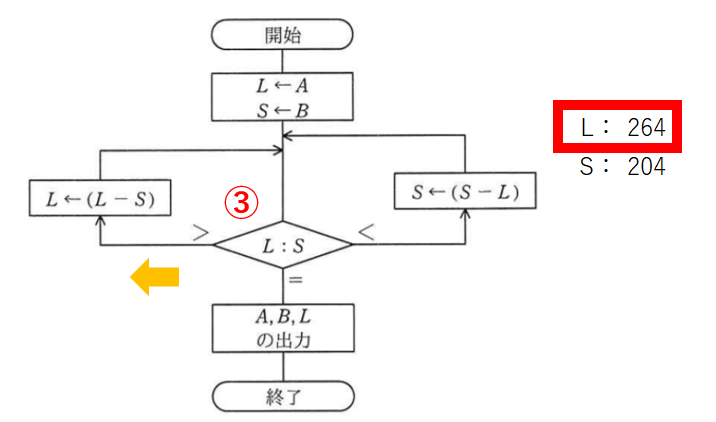
比較4回目。これも左です。
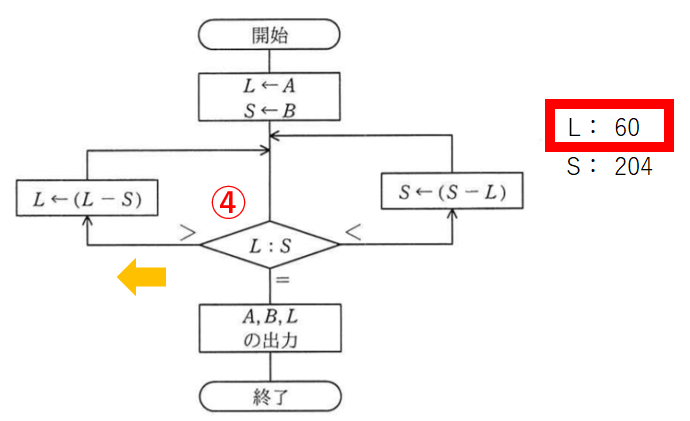
LからSを引きます。
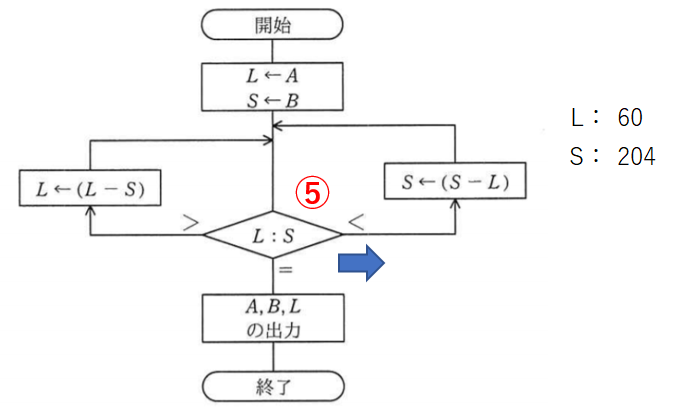
比較5回目。初めてSのほうが大きくなりました。
青矢印の右へ進みます。
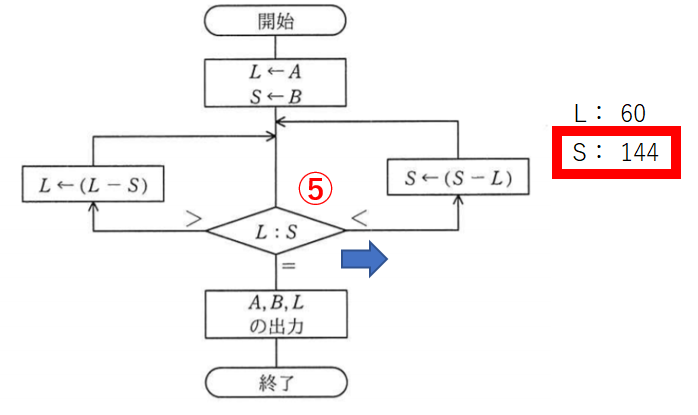
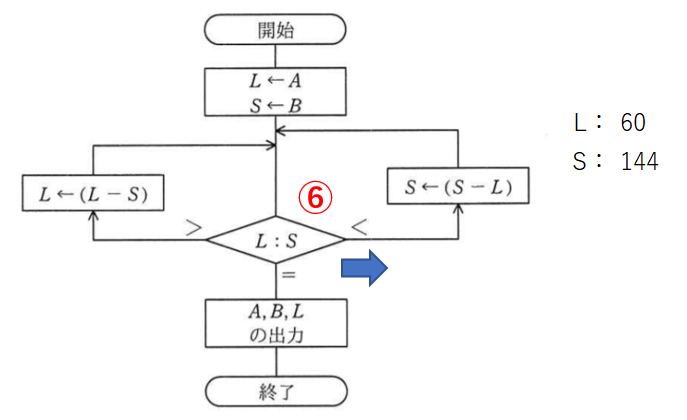
Sの204からLの60を引いてSを144とします。
比較6回目。Sの方が大きいので右へ進みます。
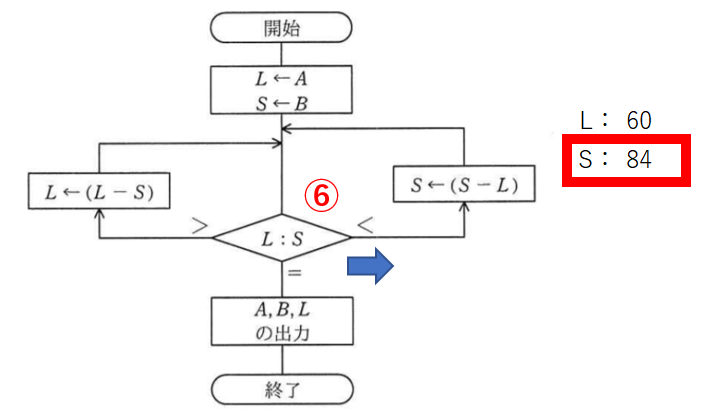
SからLを引いてSを84にします。
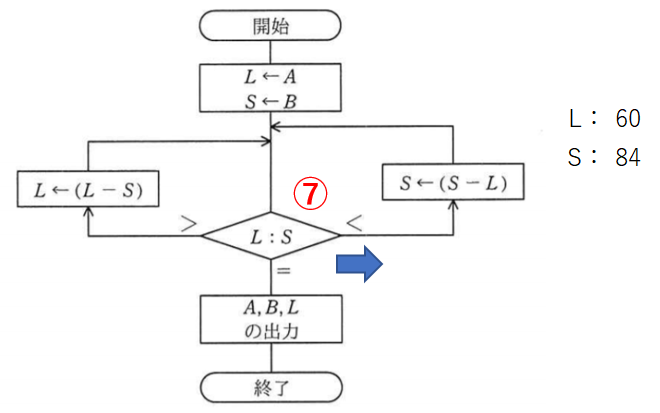
比較7回目。Sの方が大きいので右です。
ぼちぼちめんどくさくなってきてます、私。
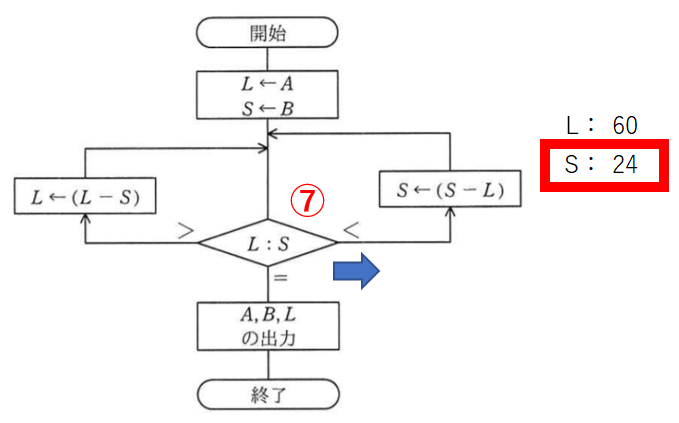
SからLを引いてSを24とします。
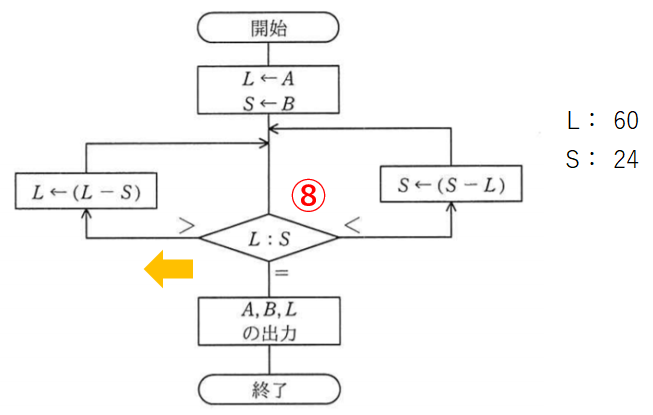
比較8回目。Lのほうが大きいので左です。
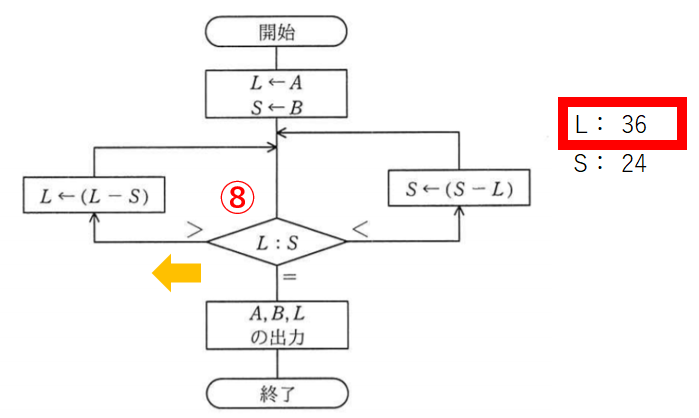
LからSを引いてLを36とします。
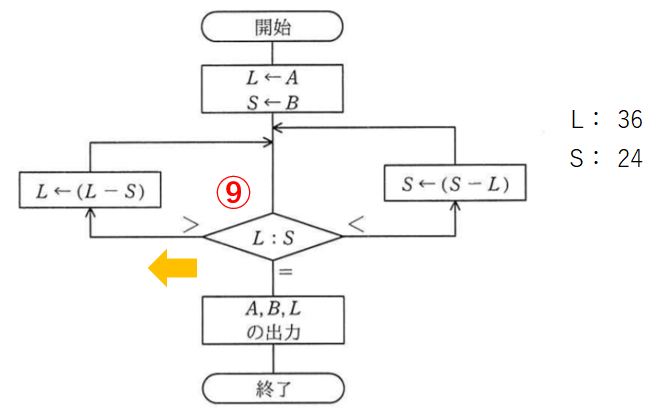
比較9回目。Lの方が大きいから左です。もう飽きた。
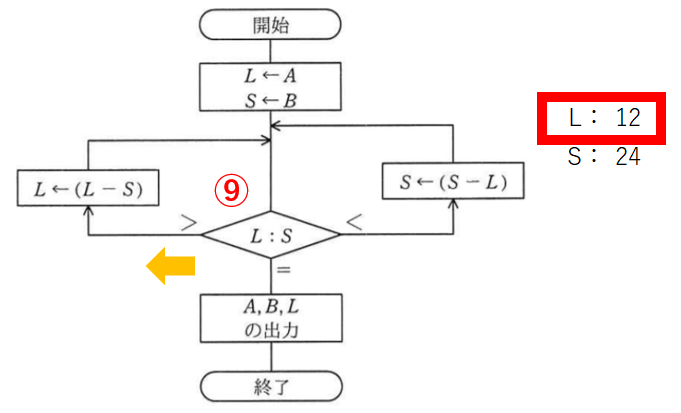
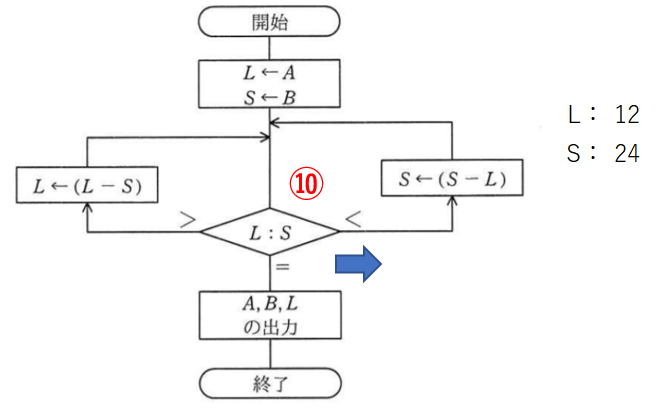
LからSを引いてLを12とします。
比較10回目。Sほうが大きいので右です。
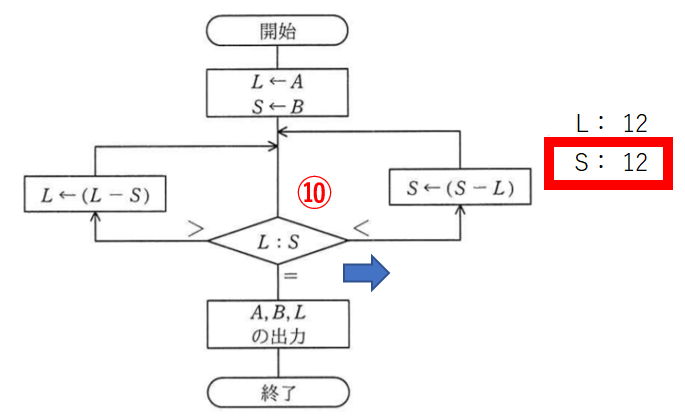
SからLを引いてSを12にします。
お、SとLが同じ数値になった。ということはついに、、、
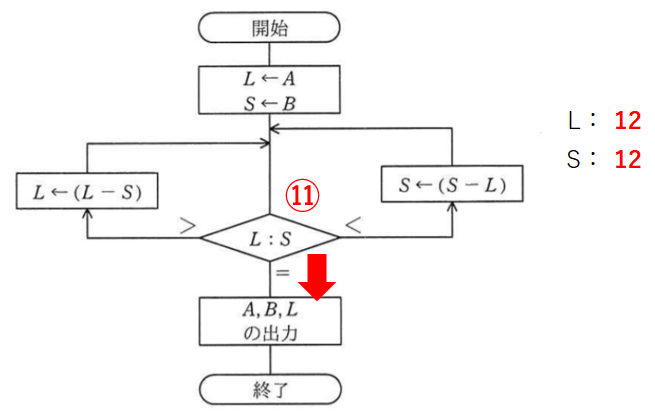
比較11回目。LとSが同じ数値になったので下に進みます。
要するに処理終了です。結果、11回。
答えは(エ)!!
正解は(エ)です。
ほら!!完璧じゃない?
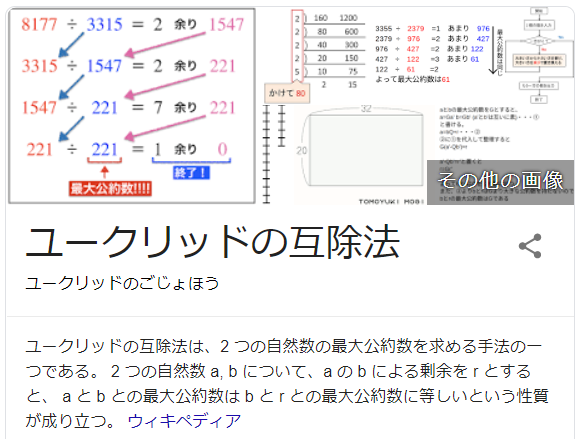
ユークリッドの互助法とは、2つの自然数の最大公約数を求める手法。
ここから私の思考です↓
計算方法としては合ってました。パチパチパチ。
ただ、ユークリッドの互助法ってのがなんなのかわかんない。
へー。
自然数aと自然数bの最大公約数は
自然数bとaをbで割ったときの余りとの最大公約数と同じなのか。
うん。へー、とは言ったものの全然ピンとこない。
まぁ覚えても日常生活や仕事では死ぬまで使わないでしょうね。
また1つ賢くなりました。よかったよかった。




コメント